Staying in place in outer space

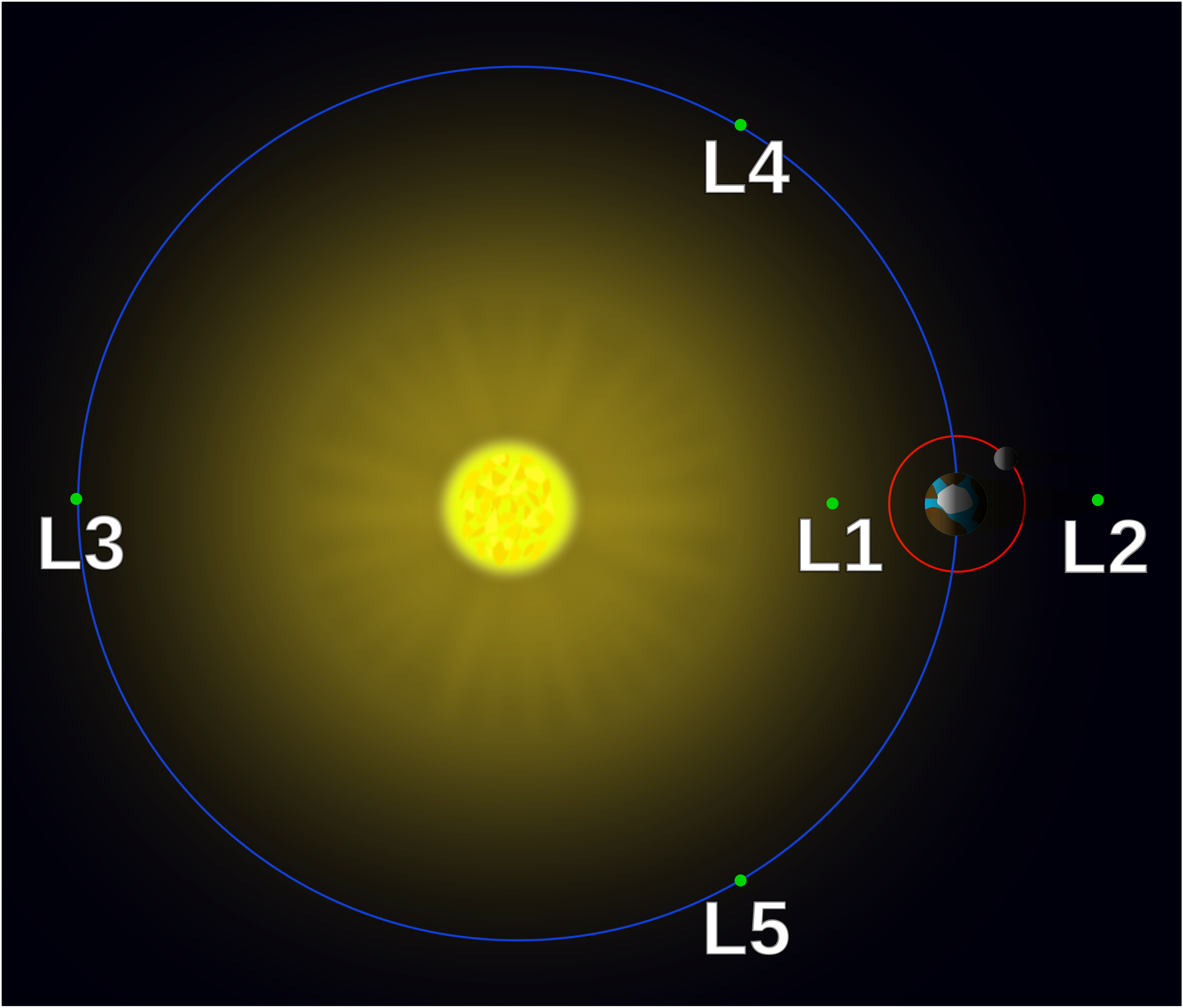
This month I learned about Lagrange points, the five locations in space relative to any two large bodies (like the Sun and Earth), where small objects (like a satellite) will tend to stay put. I first heard about Lagrange points because the James Webb Space Telescope is headed to a particular Lagrange point called the L2 point of the Earth-Sun system. A place in space where objects can remain stationary! It’s a surprising idea, and also one that turns out to be a little bit oversimplified.

Something that’s really nice about astronomy is that, due to the amount of general interest, there are tons of great resources for learning about astronomy at a high level. (NASA in particular has some excellent explainers.) But successful science communication can also belie how complex the underlying mathematics is, as well as the many assumptions made along the way.

For example, there are many high-level explanations of how the moon’s gravitational pull causes the Earth’s tides. But when you look closer, not only are there lots of equations, but these equations require a number of simplifying assumptions: “a spherical, smooth and homogeneous Earth, covered with a uniform film of water. Around that Earth, revolves a point-like Moon…We intentionally leave the Sun out of the picture…[and assume] the Earth is not rotating.” These are subtleties that can go completely unappreciated if you stick to the high-level explanations.

So, how does one get a better understanding of what Lagrange points are? Personally, I found that working my way through the math involved updating some of the basic/incorrect concepts I was taught in grade school. For instance, as you probably know, the Earth takes an elliptical orbit around the Sun. But contrary to the majority of pictures you’ll see when google image searching “earth orbits sun”, the Sun is not at the center of this ellipse—it’s at one of its foci ¹. Even weirder, the other focus is empty (“ghost”):

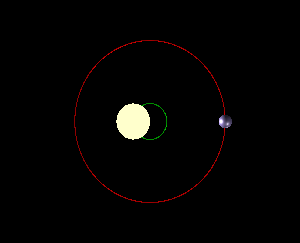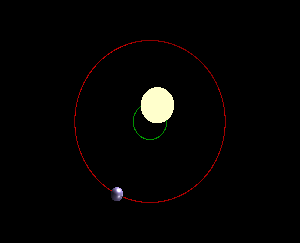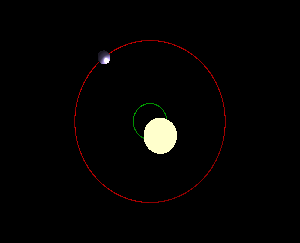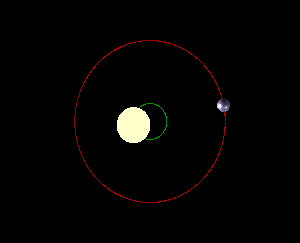
Ultimately, the idea that the Earth orbits the Sun is a simplification. In fact, both the Earth and Sun orbit what’s called the Earth-Sun barycenter, or the center of mass of the two bodies. In other words, the Earth doesn’t orbit the Sun—the Earth and Sun both orbit their barycenter! It just so happens that the Sun is so large that the barycenter is always inside the Sun, so it’s simpler to just think of the Earth as orbiting the Sun. For two bodies that are slightly closer in mass (gif below), it’s easier to see that the two bodies are orbiting their barycenter and not each other:

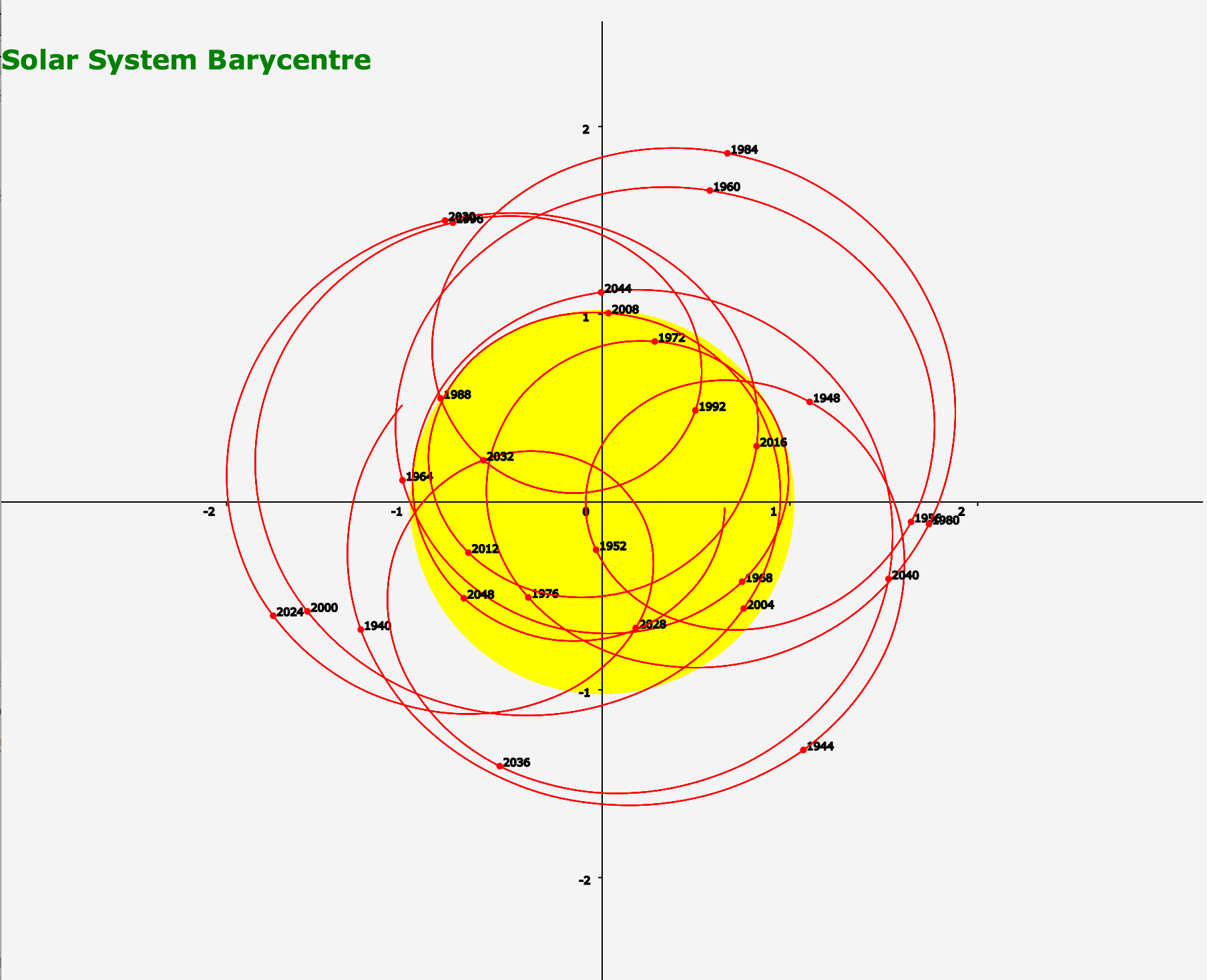
(As an aside, a similar thing is true when we think about all the planets revolving around the Sun: We pretend that the Sun’s position is fixed. But in fact, all the planets and the Sun revolve around the solar barycenter—that is, the center of mass of our solar system. Here’s a fun plot of how the solar barycenter has changed over the last century or so, relative to the Sun:)

Whenever you see a plot of the orbits of two bodies like the Sun and Earth, those orbits are a result of solving what’s known as the Kepler problem, a special case of the two-body problem where the only force acting on the two bodies is gravity ².

To understand where the Lagrange points are, we need to think about the orbits of three bodies. For example, in the case of the James Webb telescope, we have the Sun, the Earth, and the telescope. But finding the orbits of three bodies, known as the three-body problem—yes, like the book!—is a little trickier. With three or more bodies, there is no general closed-form equation for the orbits ³. But luckily, if we assume the telescope’s mass is small enough that the gravity exerted by the telescope on the Earth and Sun is negligible, we can get an equation for the the orbits in this so-called “restricted” three-body problem.

A Lagrange point is a position relative to the Earth and Sun’s positions that experiences a net force of zero. In other words, it’s a position where the gravitational pull of the two larger bodies, along with the centrifugal force ⁴, all cancel out. These are the points where, in theory, if we put a satellite, it would stay in that position forever because there would be no net forces on it ⁵. In more mathematical terms, a Lagrange point is a fixed point of the dynamical system that results from the gravitational pulls of the Sun and Earth.

But one thing not obvious from the Lagrange point picture at the start of this post is that Lagrange points are all defined relative to the distance between Earth and the Sun. This distance changes over time (because the Earth and Sun are themselves in motion), which means the position of the Lagrange point is itself changing over time. Thus, a satellite parked at, say, the L2 point isn’t really motionless. It’s just that it stays in a fixed position relative to the distance between Earth and the Sun.

---

Notes